Distancia Punto a Linea

Paso 1. Descargar la información.

Primero había que descargar la información de la frontera norte de México a mi computadora. La primera opción que pensé hacer fué filtrar las líneas superiores de un shape de los estados del país, pero si lo piensas un poco… ¿como podría decirle a R cual es la línea superior de un estado? ¿Seleccionando los puntos más extremos en el eje Y?

Pues tal vez esa podría ser una opción, pero el algoritmo de Googlear la base de la línea de la frontera y descargar la base resultó más efectivo.

Si eres de los que les dá flojera ir a la página, descargar archivos, ir a la carpeta de Descargas, y mover el archivo a la carpeta de trabajo, puedes copipegar el código que viene a continuación (obviamente, descargando primero el paquete curl del CRAN en tu sesión de R).

# Descarga datos automaticamente, si te da flojera darle cl
curl::curl_download("https://opendata.arcgis.com/datasets/e735940321bd4383bab528a91bf526f8_0.zip?outSR=%7B%22latestWkid%22%3A3857%2C%22wkid%22%3A102100%7D",
destfile = "frontera.zip")

Esto me descargó un archivo *.zip, que yo nombré como frontera.zip, en mi directorio de trabajo. Como ya caducó mi licencia de WinRar 😔 y no puedo descomprimirlo en la computadora, utilizo el siguiente código para extraer la información:

# Deszipeado
unzip(zipfile = "frontera.zip")

Una vez descomprimido, tengo ahora un montón de archivos en mi directorio de trabajo llamados Mexico_and_US_Border con distintas extensiones, tales como *.shp, *.shx o *.dbf. Estos archivos son una de las maneras en que se guardan las bases de datos geográficas (formato shapefile), y estos archivos se pueden abrir desde R con la librería sf.

Fig. 2 Archivos que conforman en shapefile de la frontera.

Paso 2. Abriendo los datos.

Para abrir la base de datos de la frontera norte, usamos la función sf::st_read() como se ve a continuación:

# Librerias
library(sf)
library(tidyverse)
# Apertura del archivo (solo abrimos el archivo *.shp)
f <- st_read("Mexico_and_US_Border.shp")

Y ya. así lo abrimos. Para corroborar que sea efectivamente un archivo geográfico, lo ploteamos (dibujamos):

Nota. Utiliza siempre el argumento max.plot=1 para explorar tus datos (si no, tu compu lo va a pasar muy mal).

# Ploteado (te recomiendo que no le muevas al max.plot = 1)
plot(f, max.plot = 1)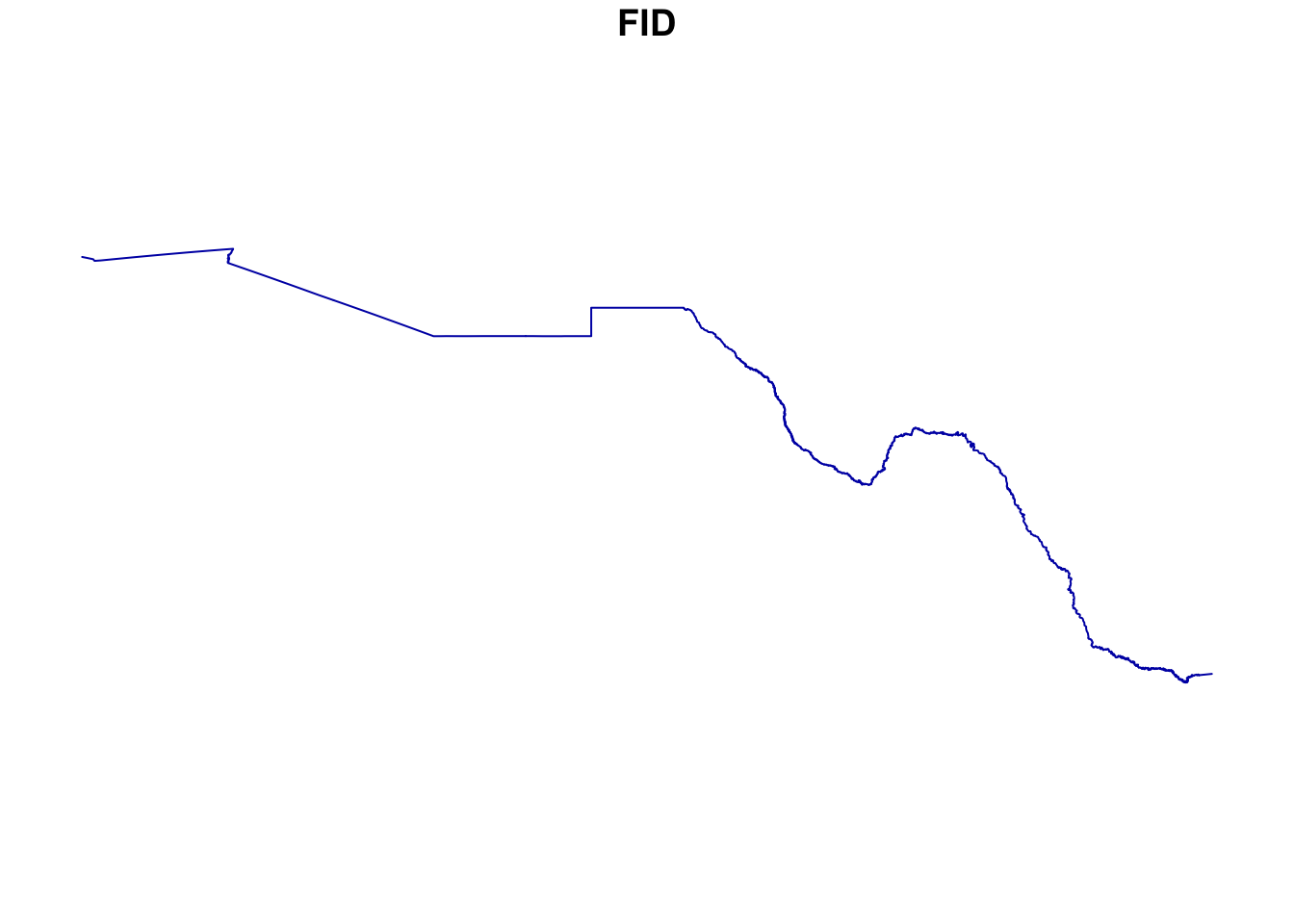

Fig. 3 Polilínea de la frontera norte

Efectivamente, tiene los datos que necesitamos.

3. Definiendo el punto.

Ahora hay que determinar el punto al cual le vamos a sacar la distancia respecto de la frontera norte: como mi amigo es estudiante del Colmex, vamos a calcular la distancia de El Colegio de México a un punto (el más cercano) a la frontera norte.

Para sacar las coordenadas del Colmex, lo buscamos en Google Maps, y le picamos encima de la biblioteca para sacar sus coordenadas:

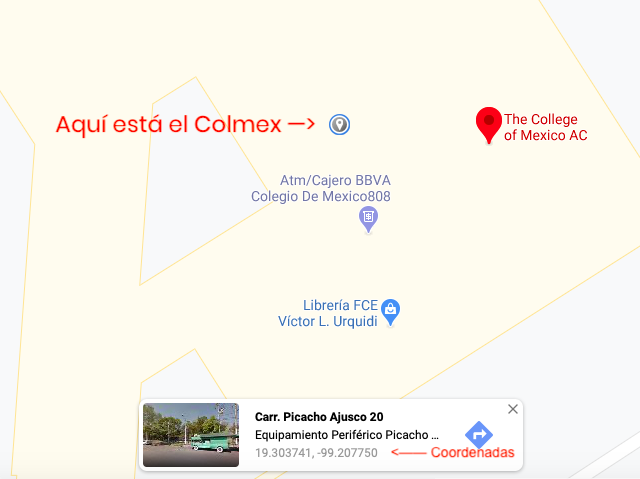
Fig. 4 Coordenadas del Colmex en Google Maps.

Ahora, creamos una tabla que almacene estas coordenadas latitud/longitud:

# Las coordenadas del Colmex en formato tabla-dataframe
pto <- data.frame(x = -99.20775, y = 19.303741) %>% 
  st_as_sf(coords = c("x", "y")) 

# Homologamos el Sistema de Coordenadas de Referencia con la base de la línea de la Frontera Norte
st_crs(pto) <- st_crs(f)

Nota. Cuando se va a trabajar con la interacción de dos bases de datos geográficas, o cuando se van a realizar mapas en leaflet, es siempre necesario homologar el Sistema de Coordenadas de Referencia, escogiendo, en este caso, el 4326 (WGS84).

4. Calculamos la distancia.

Ahora calculamos la distancia. La librería/biblioteca/paquetería sf tiene ya pre-programada una función llamada st_distance() para calcular la distancia geodésica que hay entre dos elementos geográficos del mapa. Utilizaremos esta función para calcular la distancia de un punto a la frontera.

st_distance(pto, f) 

## Units: [m]
##          [,1]
## [1,] 746695.6

Y ya, la distancia de El Colmex a el punto más cercano de la frontera norte (quién sabe cual) es de 746.6889 km ( 746,688.9 m).

Y ahí está la respuesta a la distancia, y al reto de mi amigo. Fin.

5. ¿A qué punto se calculó la distancia?

Pero ahora pueden surgir preguntas muy lógicas sobre esta respuesta… Una de ellas es: ¿A qué punto de la frontera se le calculó la distancia?

Entonces, hagamos el cálculo más detenidamente. Para esto, propongo descomponer la línea de la frontera norte en sus vértices o componentes:

# Descomponemos la linea en sus coordenadas
ptos_linea <- st_coordinates(f) %>%
  as.data.frame() %>%
  st_as_sf(coords = c("X", "Y")) 

st_crs(ptos_linea) <- st_crs(f)

class(ptos_linea)

## [1] "sf"         "data.frame"

st_crs(ptos_linea)

## Coordinate Reference System:
##   EPSG: 4326 
##   proj4string: "+proj=longlat +datum=WGS84 +no_defs"

Y ahora calculamos las distancias del Colmex a todos los vértices de la frontera norte:

# Calculo de las distancias
distancias <- st_distance(ptos_linea, pto)
# Observamos los primeros registros
head(distancias)

## Units: [m]
## [1] 775122.1 766724.1 766723.6 766720.5 766717.8 766712.2

Y ahora, sacamos la línea con la menor longitud:

# Obtencion de la distancia minima
distancia_minima <- min(distancias) 

# En kilometros
(distancia_minima / 1000) %>% as.numeric()

## [1] 746.6956

Como podemos ver, la distancia mínima es la misma distancia que calcula la función st_distance(). Ahora, ¿cuál punto de todos esos es el punto más cercano al Colmex? Para conocer esto, filtramos las distancias hasta quedarnos aquella observación que tenga la distancia igual a la distancia mínima.

# Punto minimo
punto_frontera <- 
  ptos_linea[distancias == distancia_minima,]

Y para visualizarlo, creamos una línea que va del Colmex a dicho punto:

# Linea de distancia mínima
linea <- st_linestring(matrix(c(pto[,"geometry"] %>% 
                              st_coordinates(), 
                              punto_frontera[,"geometry"] %>% st_coordinates()), ncol = 2, byrow = TRUE))

Y lo plasmamos en un mapa de leaflet:

library(leaflet)

# Hacemos el mapa 
leaflet() %>% 
  addTiles() %>% 
  addCircleMarkers(data = pto) %>% 
  addCircleMarkers(data = punto_frontera) %>% 
  addPolylines(data = linea) %>% 
  addPolylines(data = f, color = "red")

Fig. 5 Mapa de la línea con la mínima distancia

Y resulta (haciendo zoom podemos darnos cuenta) que el punto más cercano a la frontera norte se encuentra unos kilómetros al Este de la Ciudad de Matamoros, en el Estado de Tamaulipas.

6. ¿Y si quiero calcular la distancia respecto a otro punto?

Para hacerlo para cualquier punto de México, hacemos una función. Las funciones son pedazos de código que, entre otras cosas, se programan para llevar a cabo tareas repetitivas (como todo lo que hicimos arriba) variando ciertos datos de entrada. Primero, empezaremos haciendo una función para calcular solamente las distancias a la frontera.

# Función para calcular las distancias. 
distancia <- function(X, Y){
  pto <- data.frame(x = X, y = Y) %>% 
          st_as_sf(coords = c("x", "y")) 
        st_crs(pto) <- st_crs(f)
  st_distance(pto, f)       
}

Y ahora, probamos la función a tres puntos seleccionados: a Mexicali, a Puerto Peñasco, Sonora y al CIDE, CDMX.

# Distancia a un punto del mpio de Mexicali, BC
distancia(X = -115.418556, Y = 31.795112)

## Units: [m]
##          [,1]
## [1,] 96247.57

# Distancia a Puerto Peñasco, Sonora
distancia(X = -113.534104, Y = 31.309766)

## Units: [m]
##          [,1]
## [1,] 82426.91

# Distancia al CIDE
distancia(X = -99.263426, Y = 19.374515)

## Units: [m]
##        [,1]
## [1,] 740530

# Distancias a todos estos puntos 
distancia(X = c(-115.418556,-113.534104, -99.263426), 
          Y = c(31.795112, 31.309766, 19.374515))

## Units: [m]
##           [,1]
## [1,]  96247.57
## [2,]  82426.91
## [3,] 740530.00

7. ¿Y la trayectoria o línea de mínima distancia?

Y ahora, haremos otra función para dibujar las líneas. Esta función va a empaquetar todos los pasos que seguímos para determinar el punto de la frontera al cual llegaba la línea con la distancia mínima.

# Funcion para dibujar las lineas de minima distancia
# Nota, esta función da por hecho que previamente ya cargamos 
# la base de datos de la frontera y la almacenamos en el objeto f
dibuja_lineas_minima_distancia <- function(X,Y){

  # Creamos el punto a partir de los argumentos X y Y
  pto <- data.frame(x = X, y = Y) %>% 
        st_as_sf(coords = c("x", "y")) 

  # Homologamos el Sistema de Coordenadas de Referencia
  st_crs(pto) <- st_crs(f)
  
  # Extraemos los vértices de la linea
  ptos_linea <- st_coordinates(f) %>%
    as.data.frame() %>%
    st_as_sf(coords = c("X", "Y")) 
  
  # Homologamos el Sistema de Coordenadas de Referencia
  st_crs(ptos_linea) <- st_crs(f)

  # Sacamos las distancias del punto a todos los vertices de la frontera
  distancias <- st_distance(ptos_linea, pto)

  # Obtencion de la distancia minima
  distancia_minima <- min(distancias) 

  # Guardamos el punto de la frontera con la distancia minima
  punto_frontera <<- 
    ptos_linea[distancias == distancia_minima,]

  # Construimos la linea de distancia minima
  linea <- st_linestring(matrix(c(pto[,"geometry"] %>% 
                                st_coordinates(), 
                                punto_frontera[,"geometry"] %>%       st_coordinates()), ncol = 2, byrow = TRUE))  
  
  # Seleccionamos la linea como objeto a retornar de la funcion 
  return(linea)
  
}

# Probamos la funcion, sacando la linea del CIDE a la frontera
lineaCIDE <- dibuja_lineas_minima_distancia(X = -99.263426, Y = 19.374515)

# Dibujamos el mapa
leaflet(lineaCIDE) %>% 
  addTiles() %>% 
  addPolylines(color = "#005700")

Pues ahora tenemos una función que nos calcula la distancia y otra que nos dibuja las líneas. Entonces, a partir de estas funciones, cualquier programador experimentado de R puede calcular las distancias y la trayectoria en línea recta a la frontera a partir de solo tener las coordenadas X y Y del punto de interés, y copipegando las funciones de arriba en su sesión de RStudio.

8. ¿Y si hacemos un shiny?

Bueno, y ¿si hacemos una solución en la cual cualquier usuario pueda calcular la distancia de cualquier punto a la frontera sur de Estados Unidos? Esto lo vamos a lograr con la librería shiny y pegando todo el código que hemos hecho arriba.

9. Conclusiones.

Sobre los motivos…

Para alguien experimentado en el análisis de datos espaciales quizá el contenido de este artículo no le sea lo suficientemente impresionante (para mi ciertamente no lo es tanto), pero si constituyó una buena excusa para programar algo divertido e introducir varios conceptos de varios cursos que voy a dar en la Escuela de Métodos del LNPP-CIDE a lo largo de este año. Por ejemplo, la parte de descarga de datos de internet lo voy a abordar en un curso de Manejo de bases de datos no estructurados que voy a dar en Noviembre, la de elaboración de mapas en el de Análisis de datos Geoespaciales en Mayo y la de creación de Aplicaciones en shiny lo voy a dar a lo largo de el mes de marzo, todos en 2020.

Sobre el uso de los vértices…

Platicando con mi colega Juan Javier Santos, creemos que calcular la distancia a partir de los vértices puede ser un poco problemático (pensando en el caso de una línea recta a una distancia \(\epsilon\) pequeña de un punto) Sin embargo, creo que dada la cantidad de vértices y las distancias a las cuales se calculan las distancias, esto no debería constituir un gran problema.

Sobre la creación del shiny…

Igualmente, si bien el shiny se construyó en un código de 151 lineas (tampoco es tanto) la elaboración del shiny implicó hacerlo a través de múltiples pasos (primero lo boceteé, luego diseñé la interfaz, luego generé las funciones, luego afiné detalles y corregí errores y excepciones, los cuales me salieron a montones a lo largo de la programación). Tuve un error al hacer el upload, debido a que en Mac, si bien corría bien de manera local, al subirlo había cierta discordancia entre el funcionamiento de ciertas librerías, por lo que recomiendo, si se va a subir la replica a internet, subirlo en una computadora Windows (en lo que encuentro cual fué el error).

Sobre el seguimiento al post.

Si tienen dudas de alguna parte de esta entrada de blog, algún comentario o me detectaron algún error, me encuentro disponible en Twitter en @JuvenalCamposF, o a mi correo, juveroark@gmail.com.

Gracias por llegar hasta acá. :3

Juvenal Campos.